Islamic
Prayer Times -
Observation and physical aspects
Aug 14, 2009
Observation and physical aspects
Aug 14, 2009
Contents
- Summary of observations
- Reasons for the variation
- Factors affecting observation
- The observations in Blackburn, UK
- Criteria for correct observation
Observations
In order to translate fiqh definition of prayer times into angles for the sun's position relative to the horizon, which are needed for astronomical calculation, direct observations are required. Some of the available data are displayed and discussed below.
Summary of observations
In the table below we have compiled some of the observations quoted in the Muslim discussion, together with the corresponding calculated angles.
| Observer |
Location |
Latitude Elevation |
Period
of observation |
Fajr/ Isha |
Transition
between red and white twilight |
Transition
between white twilight and complete darkness |
| Hizbul
Ulama1 |
Blackburn, UK |
53.8° | Sept 1987 - Aug 1988 |
Fajr |
--- | 13.8-15.0° (winter months) |
| H.
Ghauri5 |
Montreal & Toronto |
45.5° 43.7° |
summertime |
Fajr |
14.2°-14.8° |
16.7 - 17.9° |
| Khalid Shaukat4 | Canada |
45° | ... |
Fajr |
--- |
14.5°(summer) |
| 17.2°
(winter) |
||||||
| Omar
Azfal2 |
Tracy, CA |
37.7° | July 1-19, 2005 |
Fajr | 5.9--7.0° | 10.5° 6 |
| Dr Sultan3 | Sana'a, Yemen | 15.4° 2200m |
Nov 24, 2003 |
Fajr | 13.2° (10.8°)3 |
19° (16.5°)3 |
| Estimate6 | Fajr | 11-14.5 |
14-18° | |||
| Hizbul
Ulama1 |
Blackburn, UK |
53.8° | Sept 1987 - Aug 1988 |
Isha |
8.5° | 13.5-13.8° (winter months) |
| H.
Ghauri5 |
Montreal & Toronto |
45.5° 43.7° |
summertime |
Isha |
13.9°-14.7° |
17.0 - 17.9° |
| Khalid Shaukat4 | Canada |
45° | ... |
Isha |
...
|
10.9°
6 (summer) |
| 16.1°
(winter) |
||||||
| Omar Azfal2 | Tracy, CA |
37.7° | July 1-19, 2005 | Isha | 7.5-8.2° | 10.2° 6 |
| Omar Azfal2 | Tucson, AR |
32.2° 845m |
Sept 12-17, 2002 |
Isha | 14° (13.2°)3 | 15.6° (14.8°)3 |
| Estimate6 | Isha | 8.5-14.5° | 14-19° | |||
- The angles have been obtained as the best fit to the data tabulated Blackburn. Using a single fix angle, good agreement is obtained for the entire period where the table is based on true observations, i.e. from September to March. During summer, the tables give estimated and manipulated, not those actually observed. (see this Figure).
- Angles have been evaluated from given data for observed times.
- The reported times for sunrise and sunset do not agree with
the times obtained from calculation for the given location - possibly
an effect of high altitude. If this is corrected for, the angles given
within brackets are obtained.
- Angles calculated from published tables (quoted by www.as-sidq.org).
- Angles based on observation reported.
- Very small angles may be assumed to be heavily influenced
by light contamination - see explanation
below. These values have been disregarded in total estimate.
Reasons for the variation
Publicly observations are relatively few, and there is large variation between the angles obtained from the various observations. This has led some scholars to categorically reject that there is a relation between the observed level of twilight and the sun angle. This is a wrong conclusion, as the relative movement of sun and earth is, without any doubt, correctly modeled by the astronomical equations, which Muslims have been using for over 1000 years, Hence, angles are the correct way to model twilight. Rather the great scatter may be attributed to one or several of the following factors:
- the observers were witnessing different degrees of twilight
- the observations were affected by varying levels of
background disturbances (such as light contamination)
- single day observations are quoted, which are subject to
natural day-to-day fluctuation (e.g. in refraction and/or visibility),
rather than measuring for a longer period and fitting an angle to an
entire data set.
Factors influencing the observation
What factors may be assumed to influence the observation of sunrise/set and twilight? The following is a list of possible factors that may come into play, directly or indirectly:
Background light (light contamination). Astronomical observations are very sensitive to the degree of night sky darkness. Light contamination means that the background light limits the observation, since it is only possible to observe objects or phenomena that are brighter than the background light. In the presence of background light, true Fajr and Isha cannot be observed, since morning twilight appears later, and evening twilight disappears earlier, than with a completely dark sky. The corresponding angles will then appear smaller than they would be if true darkness were seen. This is likely to be the most important factor in twilight observation. Cinzano's world map of light contamination shows which regions in the world are most affected. In the extended large city extended around San Francisco, where the observations of Dr Omar Azfal were made, light contamination is likely to be a major factor, and it is not at all unreasonable to see twilight disappear when the sun is only 10° below the horizon, as exposed in detail in the section Quantifying darkness. It is not sufficient in such areas to move 30-50 miles out of the city kernel - light contamination will still be present.
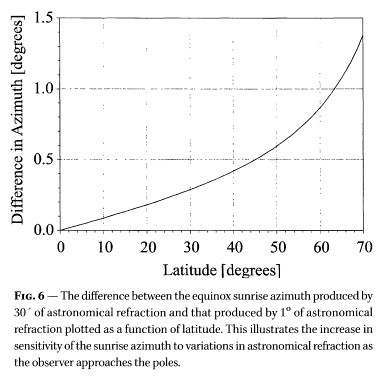
Refraction. Refraction varies with latitude and atmospheric conditions. Due to this, we would expect about 1° higher twilight angles at the polar circle compared to the equator. Seasonal and day-to-day fluctuations should also be expected. Refraction is slightly larger in summer than in winter (see figure below), and so is the level of fluctuation. Seasonal variation could be estimated to less than 0.5° n an average, while day-to-day fluctuation may be up to 1.5°.
Haze and aerosols in the atmosphere have a large impact on twilight colors. This has attracted the attention of environmental scientists and astronomers, who use the color spectrum to evaluate the amount of aerosols. This is likely to affect the observation of transition between red and white twilight. Observation of transition to darkness is only affected insofar as the haze decreases the visibility which would yield smaller twilight angles.
Obstructed horizon. If observation is not made at a free horizon, one will observe twilight appearing/disappearing at too late/early time, and the resulting angles will be reduced by an amount corresponding to the apparent bow length of the obstruction at the horizon. If e.g. twilight is observed above a forest with an apparent height of 5°, the observed twilight angles will be 5° less.
Elevation above sea level. The observer's elevation above sea level directly affects the angle at which the sun or its remaining rays are observed, however it is not clear exactly in what way. If the observer's position is higher than the horizon he observes, his field of view is exapanded in a way that is accounted to by introducing a factor proportional to the square root of the elevation difference into the equations. This is discussed here. However, using this correction does not yield the correct result. Another factor effect discussed in astronomical articles is the displacement of the atmospheric layer by earth elevation, which alters the refraction and deviates the incoming light rays. So far, there seems to be no easy-to-implement model of this phenomenon. Judging from observed data of sunset/sunrise, this effect would be linear with height rather than square root, and it would account for an angle alteration of 2-3° at high altitude (see e.g. the data of Dr Sultan quoted in the table above).
Adaption of the observer's eye to darkness. One may notice in the above table that observation of dawn gives higher angles than observation at night. This is natural, since at dawn the eye is adapted to darkness, and therefore more sensitive to the faint light of dawn. In the evening, in contrast, the process observed is brightness moving to darkness, and the eye, which needs 15-20 minutes to adapt to new light condition, is constantly lagging behind. Twilight passes quicker near the equator than near the poles, since the sun rises and sets more vertically. E.g. the time difference between 15° and 18° is about 10-15 minutes around the tropical circles compared to 30-80 minutes (depending on the season) near the polar circles. This gives the eye more time to adapt, and one would therefore expect less dawn/dusk assymmetry near the poles. as well as less scatter in the observed times. This effect may account for a difference of typically 1° or less.
Latitude. There is no reason to believe that latitude in itself would affect the observation of twilight. However, a series of factors come into play indirectly, as they vary with latitude. (a) The speed of the twilight process - (b) Refraction varies (on time average) from 0.5° at the tropical circles to 1.3° at the polar circle. - (c) Light contamination is significant in most part of the industrialized areas on the northern hemisphere, while on the southern hemisphere it is confined to a few large cities, see Cinzano's world map of light contamination.
Season. According to the astronomical model, there is no variation in twilight angle with season. However, many observations tend to tend to give about 1° higher twilight angles in summer than in winter (see for instance the tables of Dr Shaukat). A possible explanation could be that light contamination is less in summer, when night falls at a later hour, another could be seasonal variation of the atmospheric refraction.
To sum up: by far the largest effect is that of light contamination, which may account for a decrease of up to 8° in observed twilight angles. With this in mind, one should read the above table with a conscious bias and give more weight to reports that yield larger angles.
The observations in Blackburn
The largest study reported to our knowledge is the one conducted by Hizbul Ulama Sept 1987-- Aug 1988 in Blackburn (Latitude 53.8°). Analysis of the reported data yields the following twilight angles:
- 13.5 -- 15.0° for Fajr
- 13.5 - 13.8° for al-shafaq al-abyad
- 8.4° for al-shafaq al-ahmar
We have plotted the data given in the prayer time tables published for Blackburn (see e.g. diagram for Fajr times), and found that the astronomical model fits the data very well, except for the seasonal variation mentioned above. The observations are most probably affected by light contamination, as Blackburn is located in an extended urban area where the magnitude of the night sky brightness can be estimated to less than 21. This would make it impossible to observe changes in darkness when the sun is below 14° (compare night sky magnitudes to twilight magnitudes in the section Quantifying darkness below).
Criteria for accurate observation
There is a great need for well documented twilight observations at high latitudes, which could form a solid basis for prayer time calculation. To list some of them:
(a) verification of Fajr and Isha twilight angles at latitudes 40°-65°.
(b) verification of refraction compensation at varying latitudes
(c) seasonal variation of refraction
(d) effect of altitude on observation of sunset and sunrise
For observations to be of general value in modeling, the results must be reproducible, i.e. it must be possible to do them again in a similar setting with similar results. This requires among other things that observation be conducted:
- during nights free of haze,
clouds or moon light (note that moon light may affect night sky
brightness even if the moon is below the horizon)
- at a location with free horizon - or with measured bow angle of obstruction
- free from light contamination
- or with known background light magnitude (Fajr and Isha can
only be observed with complete darkness)
- for a period of time, or on a set of similar occasions, large enough to eliminate day-to-day fluctuation
- one must make sure that the same
phenomenon is observed for the entire period or at the various occasions
- Exact location, elevation above sea level, and position of the horizon relative to the observer
- A description of the surroundings (vegetation,
hills, remote light sources etc.)
- Weather, temperature, air humidity
- these factors affect refraction
- Magnitude of background light
can be estimated by naming the stars in Ursa Minor or Orion that are
visible when complete darkness is observed.
- A description of the observation routine
- A description of the observed
twilight process in text or pictures related to precise timing.
Many of the observations quoted in here could be criticized from this point of view, as reports are not detailed enough to allow an assessment of light and view conditions, atmospheric conditions affecting light transmission, or even precise information about the location.
Dr Hakeem-Ullah Ghauri, in the article accompanying his observation report, gives a detailed list of factors to be observed. He suggests moving 30-80 km away from the city in order to observe Fajr and Isha. As will be seen in the sky light maps below, this may not be sufficient.
Dr. Ghauri also adds another requirement, namely impartiality of the observer. He gives detailed suggestions for the observation routine in order to eliminate bias from side of the observer(s), such as absence of communication between different observers during the observation process, unawareness of absolute time etc.
Further there are some fiqhi points on observation that need to be taken into account:
- Observation by a single person is valid for that person only on the occasion of that precise prayer time, without need to take into account any of the above, except clowdines.
- Observation that will serve as a guideline for the community must be conducted from the highest point of that community's surroundings.
- Two observers (male or female) should agree on the observed time.
Quantifying
darkness
Observation of sky phenomena are highly sensitive to the background darkness. Light contamination bars the observer from distinguishing faint objects. This is also what happens when Muslims try to observe the "white thread of light" at Fajr and Isha - if there are background lights, what will be actually observed is a later stage of dawn or an earlier stage of evening twilight, and the associated angels or depression will be smaller. It is therefore necessary to quantify the level of darkness of the night sky.
Magnitude of observable stars as a measure of darkness
Astronomers use a simple way of estimating the level of darkness of the night sky: they look at constellations containing stars with a magnitude around 6 (the faintest starts distinguishable by the bare eye), and check their visibility. The constellations used are typically Ursa Minor and Orion. Ursa Minor contains stars with magnitudes between 2 and 6 (the larger the magnitude, the fainter the star), among them the polar star which has a magnitude of 2.1. The faintest stars in Ursa Minor ( δ and η ) hare a magnitude of 5. If these are visible, the night sky is fairly dark. Orion is another constellation often used to test the level of night sky brightness. On this site you can find an interactive animation showing what Orion looks like for visibility of varying magnitude, depending on the observer's latitude.
In most populated areas on the northern hemisphere, one may never see any sky objects with a magnitude 6, due to heavy light contamination from the cities. The map below shows the magnitude of visible stars in Europe. It shows that objects with magnitude 6 can only be observed (with the eye) in the mountain regions of north Scandinavia and southern Spain. In large city areas, the magnitude limit is 4 - 5.
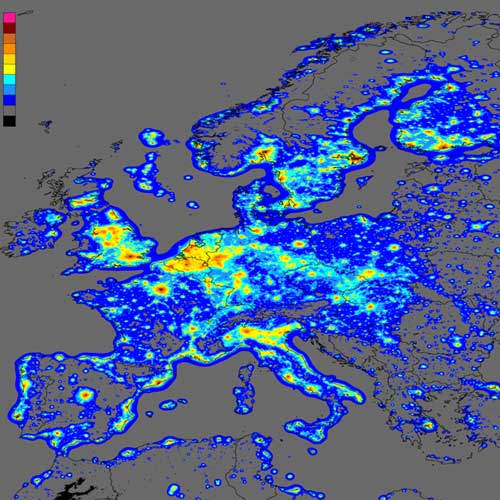
Credit: P. Cinzano, F. Falchi (University
of Padova), C. D. Elvidge (NOAA
National Geophysical Data Center, Boulder). Copyright Royal
Astronomical
Society. Reproduced from the Monthly Notices of the RAS by permission
of
Blackwell Science.
|
>6.0 |
black |
5.25-5.5 | light blue | 4.5-4.75 | golden yellow | 3.75-4.0 | red |
|
5.75-6.0 |
grey |
5.0-5.25 | azure | 4.25-4.5 | orange | <3.75 |
violet |
|
5.5-5.75 |
blue |
4.75-5.0 | yellow | 4.0-4.25 | dark orange |
Direct measurement of twilight sky brightness
Astronomers interested in assessing the quality of an observatory, or looking for suitable places to locate observatories, study the light of the level of background light on the night sky. The diagram below shows the magnitude of the violet light through the twilight process (the horizontal axis shows the sun's depression from zenith) at two observatories, Paranal in Chile (25th latitude) and CrAO on Crim (45th latitude), in clowdless and moonless nights. It is seen in the diagram that the curves level out when the sun's depression is about 15-16° below the horizon. Beyond this angle, it is not practically possible to detect any change in brightness. (Note however that the measurement was done at the highest point of the sky, not at the horizon).
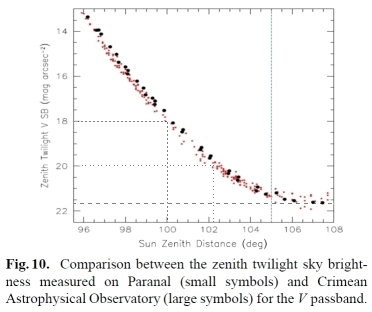
Ref: Patat, Ugolnikov and Postylyakov: UBVRI twilight sky brightness at ESO-Paranal, Astronomy & Astrophysics Manuscript, 2008 (linjer inlagda av författaren till denna artikel)
The magnitude at which the curves level out indicates the magnitude of background light, which in these two locations (Paranal and Crim) is 21.5 V mag/arcsec2, and this marks the limit of observable objects.
Observable twilight angles depending on night sky brightness
In many parts of the world, the magnitude of night sky brightness is substantially smaller than 21.5 V mag/arcsec2. The map below shows the magnitude of night sky light in Europe. It is seen that in densely populated regions this magnitude is above 19-20 V mag/arcsec2 (yellow), and around large cities 18 V mag/arcsec2 (red). It we compare this to the diagram in the previous section, we see that with a night sky background light magnitude of 18, "darkness" will be observed when the sun's depression angles is only 10°. If the background light is of a magnitude of 20, "darkness" will be observed at about 12°. In order to observe true Isha, it is necessary to be in a place where the background light magnitude is at least 21.5. In Europe such locations are the mountain regions in northern Scandinavia and Scotland, which would be ideal for twilight studies.
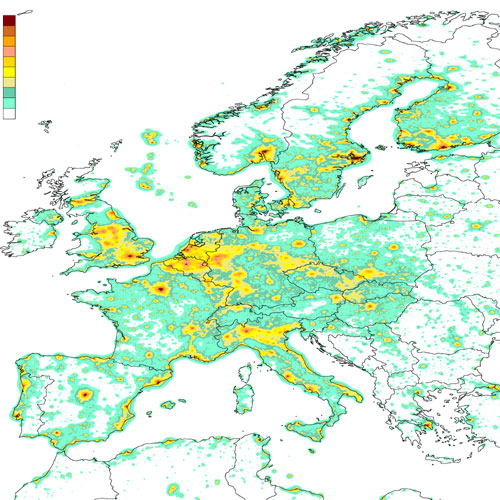
Credit: P. Cinzano, F. Falchi (University of Padova), C. D. Elvidge (NOAA National Geophysical Data Center, Boulder). Copyright Royal Astronomical Society. Reproduced from the Monthly Notices of the RAS by permission of Blackwell Science.
|
>21.5 |
white |
20.5-21 | darkgreen | 19.5-20 | yellow | 18.5-19 | pink | 17.5-18 | maroon |
|
21-21.5 |
green |
20-20.5 | kaki | 19-19.5 | darkyellow | 18-18.5 | orange | <17.5 | darkred |
Conclusion
Cinzano et. al. write the following conclusion to their article:
"93 per cent of the United States population, 90 per cent of the European Union population and about 40 per cent of the World population live under a zenith night sky that is brighter than they would have in the same location with a first quarter moon at 158 elevation (based on Krisciunas & Schaefer 1991) and zero light pollution. They therefore effectively live in perennial moonlight. They rarely realize it because they still experience the sky to be brighter under a full moon than under new moon conditions. We also found that for about 80 per cent of the United States population, two-thirds of the European Union population and more than one-fourth of the World population the sky brightness is even greater than that measured on nights close to full moon in the best astronomical sites (e.g.Walker 1987). ‘Night’ never really comes for them because this sky brightness is slightly larger than the typical zenith brightness at nautical twilight (Schaefer 1993)."
Modeling the
effect of atmospheric refraction
on observation of sunrise and sunset
on observation of sunrise and sunset
The deviation of light rays when passing through earth's atmosphere makes the sun appear above the horizon while it is, geometrically, still below. Refraction even makes it possible to see the sun during polar nights, and to observe midnight sun at locations slightly below the article circles.
Astronomical tables of sunrise and sunset as a standard use a compensation of 0.34´ (0.56°), which was suggested by F.W. Bessel in 1823 CE. Islamic prayer time tables have followed this standard.
More recent studies show that the effect of refraction can be substantially larger, especially at locations near the poles.
Empirical model for latitude dependence of refraction
Refraction is caused by variation in the air density through the atmospheric layer, which in turn depends on surface temperature, weather and atmospheric conditions, which vary with climate and season of the year. The effect of refraction on the observed time for sunrise/set will also depend on the angle at which the light rays travel through the atmosphere.
This latter effect - i.e. the latitude dependence of refraction - is shown in the below diagram, which is based on data observed for sunrise and sunset times obtained from weather sonds. The study was conducted in Edmonton, Canada (Latitude: 53.5°). It is seen that refraction gives an increase in the oberved sunrise/set angle of about 1° at latitudes below the polar circle (67°). At higher latitudes, the effect increases dramatically.
Ref: Sampson
et.al.: Variability in the
Astronomical Refraction of the Rising and Setting Sun (Edmonton),
Astronomical Society of the Pacific, 115:1256–1261, 2003 (alternate
link)
A simple curve fit to this diagram gives the function
f(Lat) = 0.59 ln ( 1 -
Lat / 78° )
which is a good approximation at all latitudes from the equator up to 75°. Sunrise/set occurs when the center of the sun is 0.27° + f(Lat) below the horizon (0.27° accounts for the passage of the sun disk radius through the horizon).
Variation of refraction due to other factors
Fluctuationa of refraction due to other factors lead to a large level of scatter around the calculated values. The below graph, taken from the Edmonton study, shows that the refraction angle in Edmonton is 0.67¨ on an average, in ageement with the above function. The level is slightly larger at sunrise than at sunset, and also the level of fluctuation is largest at sunrise.
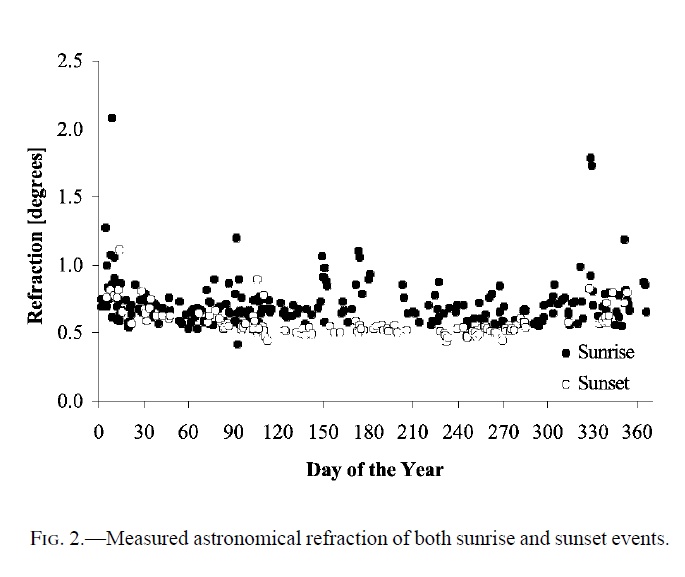
Ref: Sampson
et.al.: Variability in the
Astronomical Refraction of the Rising and Setting Sun (Edmonton),
Astronomical Society of the Pacific, 115:1256–1261, 2003 (alternate
link)
The standard deviation for all measurements in this study was 0.17°, and the scatter is largest in midwinter and midsummer. This may be due to the fact that the inclination of the sun's path to the horizon is largest at these two points of the year, making accurate observation more difficult, rather than fluctuation in the actual refraction.
Extreme refraction
At latitudes higher than 75°, with refraction angles above 1.7°, extreme refraction phenomena can be observed, such as mirages, deformation and splitting of the sun disk. In some cases the sun can be seen when it is still several degrees below the horizon. These effects, termed the Novaya Zemlya-effect, are not accounted for by this simple model.
At latitudes higher than 75°, with refraction angles above 1.7°, extreme refraction phenomena can be observed, such as mirages, deformation and splitting of the sun disk. In some cases the sun can be seen when it is still several degrees below the horizon. These effects, termed the Novaya Zemlya-effect, are not accounted for by this simple model.
References